*
THE MEASURE FORMULAE
A mathematical method
The calculus, discovered simultaneously by Leibniz and Newton, is an important technical device which greatly enlarges the scope and power of the fourfold analysis. Since it is a foundation for the argument to come, I should describe it briefly.
The concept of the calculus consists of the recognition that, besides the measurement of space and time, we may also employ the ratio of space to time; that is, speed, or velocity. In these days of high-speed travel, it is difficult to understand why the discovery of a formal expression for such a household word as "velocity" raised such a fuss. But Bishop Berkeley, the philosopher, insisted that Newton's "fluxions," which were the ratio of an infinitesimally small increment of distance to an infinitesimally small increment of time, were "logical absurdities." "For," said the Bishop, "an infinitesimal is bad enough, but a ratio of infinitesimals is preposterous."
The person who insists he was not driving sixty miles an hour because he was traveling for only ten minutes is using the same reasoning.
Newton's great discovery was that we can speak of a velocity as having instantaneous value at a point, despite the fact that to measure velocity we have to take a finite distance and divide it by a finite interval of time.
Newton
went further. "Not only may we speak of the rate of change of
distance with time, which is velocity," he said, "but we
may speak of the rate of change of velocity with time, which is acceleration." Velocity is expressed as dl/dt, which means the
derivative (or ratio) of length (distance) with respect to time (dl signifies
an arbitrarily small increment of length, dt an arbitrarily small
increment of time); acceleration is expressed as (d/dt)(dl/dt), the
derivative of a derivative, or ![]() As position is
measured by length (l), we will
As position is
measured by length (l), we will
use the words interchangeably.
The calculus enabled Newton to solve the problem of planetary motion. Even more significant is the fact that the calculus, through its concept of derivatives, is able to give a precise definition to elusive notions like force, and hence makes possible the whole science of motion.
In following the use of the calculus to explore the four categories of knowing, the non-mathematically grounded reader should not permit a horror of formulae to spoil what can be an interesting adventure. Readers familiar with mathematics will hopefully be tolerant if their equipment is borrowed for a purpose that takes it beyond its usual employment.
To illustrate the interrelation of the concepts of the calculus - position, velocity, and acceleration - let us take the example of a swinging pendulum.
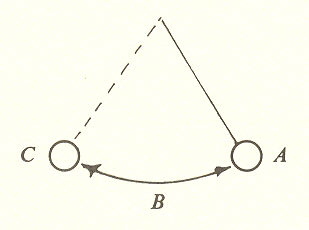
Assume that the bob of the pendulum is released at point A and swings from A through midpoint B to point C opposite A and back again. When it is to the right of midpoint B, its position is positive; when to the left, negative. A and C are thus its maximum positive and negative positions.
If we chart the position of the pendulum with respect to the passage of time, we may refer to the completion of one swing to the left and its return to A as a cycle of action, the halfway point of which is C and the first quarter of which is midpoint B. The third quarter will be B again but, to distinguish the midpoint of the return swing from that of the outgoing swing, the latter is called D. This can be represented by a new diagram on which the right and left positions of the pendulum are represented by a vertical distance above and below a horizontal line upon which A, B, C, D, A' represent successive time intervals.
This vertical distance, or swing, will be maximum positive at A, zero at B, maximum negative at C, zero at D, and back to maximum positive at the end of the line, A'. A smooth curve is drawn through these points.
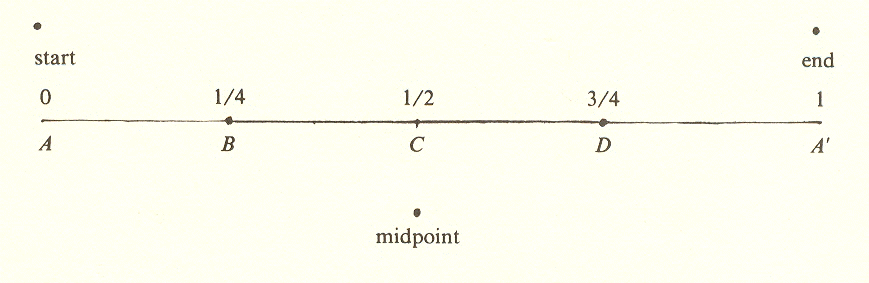
Note the slope, or "steepness," of this curve, which represents the rate at which the position changes.* At A it is zero (fiat) because the position of the pendulum is changing very slowly; at the 1/4 point B, the slope is steep and downward (negative), at midpoint C it is zero again, at the 3/4 point D it is steep and upward (positive), and at the end it is again zero. These values are marked on the same diagram to obtain a new curve, which represents the value of the slope of the first curve.
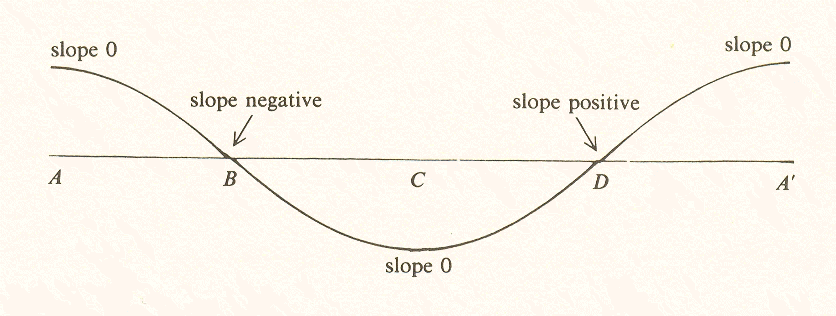
*If we take a short section of the position curve, for example, where it first crosses the line, we can see that slope is the ratio of the vertical distance dl to the horizontal distance dt. and this ratio has a definite value.
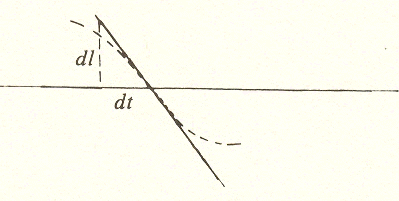
In the diagram we have made dl and dt large for visibility. But when dl and dt are large, the curve between them is not a straight line. However, if we make dl and dt small enough, the curve between them will approach a straight line, and the slope of the curve at point B will equal the ratio dl/dt, which is called the derivative of
l with respect to t. Since l is distance and t is time, dl/dt is velocity. This was Newton's discovery. It permits us to deal with an entity that is not an immediate fact of sense experience. (Since an instantaneous picture of the pendulum would not reveal its velocity or even that it is moving, we have to take at least two pictures and plot their relationship.)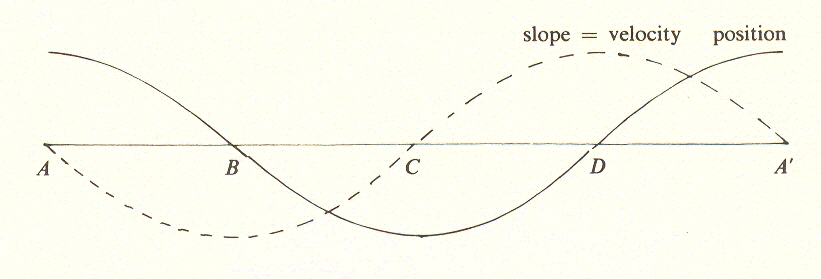
This second curve, showing the rate at which the position changes, depicts the velocity of the pendulum. Since position has been designated as positive when the pendulum is to the right, velocity is negative (moving to the left) in the first half of the swing. This is shown by the curve of velocity being below the line in the first half.
Going a step further, the slope of the velocity curve, which is to say the rate at which velocity is changing, is charted. This produces a third curve, which represents acceleration.
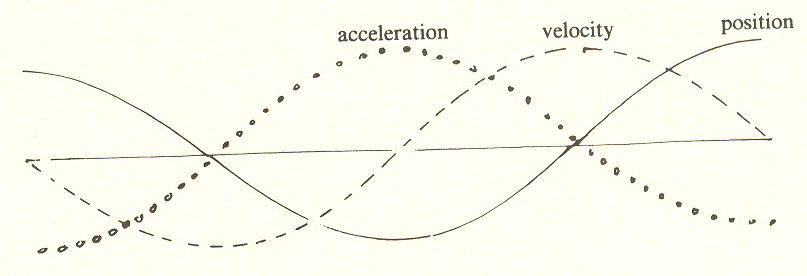
Observe that the acceleration curve is exactly opposite to the position curve. At the start, position is maximum and positive, acceleration maximum and negative. One may experience this by holding the pendulum at position A (positive), and feeling it pull back (negative). The pull is acceleration. If one lowers the pendulum into a vertical position, this pull reduces to zero (at B). The pull becomes maximum and positive (pulling toward A) when in position C and so on.
Note that these curves are all of the same shape but the curve for velocity is displaced 114 of a cycle* back from the position curve, and the curve for acceleration is displaced 114 cycle back from the velocity curve and therefore 112 cycle from the curve of position. Acceleration is thus "out of phase" with position by 112 cycle. Velocity is out of phase with both acceleration and position by 114 cycle. Note that the peak of velocity comes at D, acceleration at C and so on.
*A to A' is a full cycle, so A to B is 1/4 cycle.
The cycle of action
To take a final step, the cycle of action is represented as a full circle. To do this, we simply bend the line ABCDA' around into a circle, with A' falling on A, and the points of maximum positive position, velocity, and acceleration falling on three points 90 degrees apart.
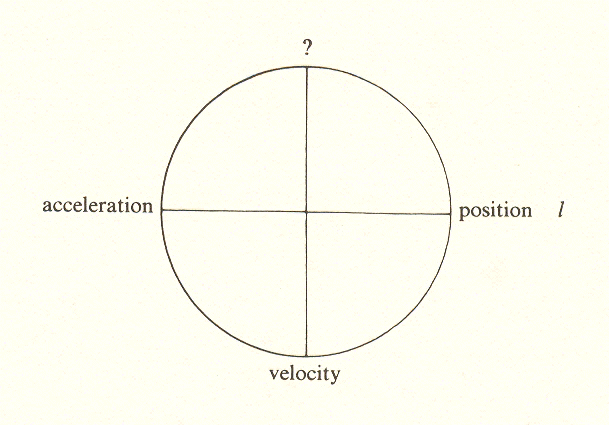
This charting presents the phase relationship between the three measures under discussion. Velocity lags behind position by 90 degrees, acceleration by 180 degrees, making acceleration opposite to position. The fourth point on the circle has no measure assigned to it. What could this measure be?
Since
it is 90 degrees "beyond" acceleration, and each right angle has
signified an additional derivative of position, we could expect it to be
the third derivative, ![]() That is to say, the rate of
change of acceleration.
That is to say, the rate of
change of acceleration.
But what name and what meaning can we give to this?
The name given to the third derivative by aeronautical engineers is jerk, probably because when acceleration is changed by an automatic control, it does so in an all-or-nothing fashion which results in a jerk. But in the general case, as in human control, it need not be a jerk.
In any case, because this control factor is not described in the textbooks, we should give it special attention. Let us take the case of driving an automobile.
To increase the speed of an automobile, we push on the accelerator, causing positive acceleration. To decrease the speed, we step on the brake, causing negative acceleration. We may also alter the direction of the car by steering.* What is the process by which the accelerator, brakes, and steering change the acceleration of the car? Clearly, a change of acceleration is what we mean by the word control, which now goes in the diagram's fourth position.
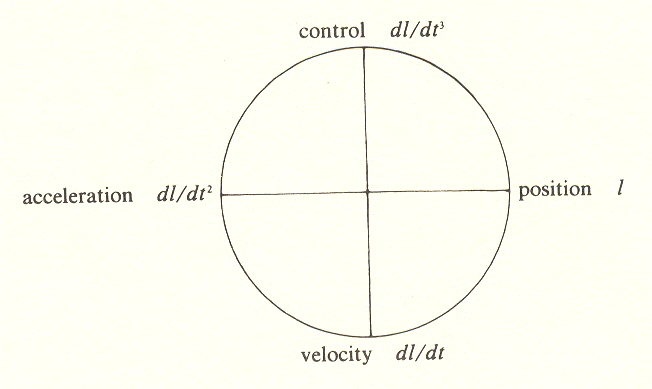
Reading clockwise, each measure is the change of the one before. This raises a question: what factor changes control?
*This is also a change of its acceleration, which may be understood as follows: Suppose we are traveling at a constant speed and make a U-turn without slowing down. We are now moving in the opposite direction, and our velocity, as measured from a point outside the vehicle, has changed from positive to negative. As this implies, a change of direction of velocity is, in fact, an acceleration. The force of this acceleration is what pushes objects in the car toward the outside of the curve. If we hold the wheel in one position so that the car travels in a circle, we are not changing the acceleration - we have simply imposed a constant acceleration.
What causes us to turn the automobile, or start it in the first place, or finally to stop it? The answer is "the destination." The destination is a place, or position. Thus the fifth step, the fourth derivative of position, that which determines control, is the same as the first step. This position is not the same position we started with but has the same category of measure (distance, or length), just as the direction in which the traveler wants to go is not a new category in the example of the map.
The examples of the map and the automobile both demonstrate the sufficiency of four categories. We need no fourth derivative. Position and its three derivatives are sufficient for analysis; and, I might add, necessary when there is control, human or otherwise.
It may be recalled that the problems of classical mechanics always exclude the possibility of a free agent "interfering with" the system. These problems employ only position and its two derivatives, velocity and acceleration, and in the case where friction can be ignored, may even omit velocity (for friction depends on velocity).
Thus the basic predictive equation that is used for treatment of the motion of all bodies, from atoms to spaceships, is:
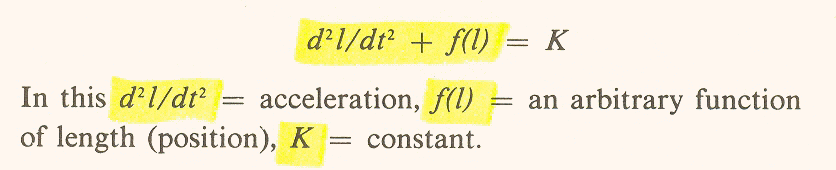
The presumption in excluding a free agent is that there could be no prediction in such a case - the equation would be too complicated or would not apply.
However, the above argument shows that there is a formal expression which covers the "free agent," namely, the third derivative. This, of course, does not mean that prediction is possible. On the contrary, it means that freedom (or unpredictability) is part of the system. In certain cases, prediction is theoretically possible, as in the case of feedback wherein a predetermined position regulates control. One example of this is a target-seeking missile - but even here, although the control is not itself free, it has been set in advance by an agent who is free to choose the target.
One might suppose such a situation altogether too complicated for complete analysis, but at least it can be shown that the four categories are again sufficient:
1. To know the position of a body in space, we need one instantaneous observation (for instance, the photo finish of a race).
2. To know its velocity, which is computed from the difference in position of the body and the difference in time between the two observations, we need two such observations.
3. To know its acceleration, we need three observations.
4. To know that a body, for example, a vehicle, is under control, and thus distinguish it from one in which the controls are stuck, we need at least four observations. That is, we need three to know acceleration and one more to know that acceleration has been changed. (This still does not tell us the body's destination or goal.)
5. To know the destination, provided the operator does not change his mind or try to fool us, we need five observations.
6. To know the operator has changed his mind or is trying to fool us, we need six observations.
Note that the fifth observation is to establish a position (the destination) and the sixth a change of position. Thus categories five and six repeat the cycle, the fifth falling into the position category and the sixth into the velocity category. As in the case of the map, the sufficiency of four categories is demonstrated.
Use of the measure formulae
We have shown that the motion of a body, even one controlled by an operator, may be formally described by the four categories of measure. The form we have used to represent these measures is that employed in the calculus:

There is an alternative, and simpler, representation in which the d's are omitted and capital letters employed; thus:

This is the form used in so-called measure formulae, the ten formulae used in physics to describe the motion of a body. Since I will discuss these formulae at some length, I will use the simpler representation.
In describing these measures - position and its derivatives we have sought to establish:
1. That four categories of measure are necessary and sufficient for the analysis of motion of a moving body.
2. That the graphic representation of these measures as four right angles dividing the circle has a special significance - each right angle is a phase shift of 90 degrees and correlates with the derivative of the one before.
In the course of the above demonstration, we uncovered another point which has philosophical significance and suggests further implications:
3. That the measure technique of science can be extended to include free will, an aspect of a situation generally thought of as nonscientific.
What is going on? We have been standing on the sidelines watching the scientist ply his trade with some technical measurements that do not appear to concern philosophy; they are just the tools of his trade. But one of these, the third derivative, turns out to be the very thing discredited by science - the human, or free will, factor!*
*It has been suggested that rather than saying the third derivative is free will, I should say that the third derivative is where free will enters - but I would protest that this implies free will is something more than control.
Perhaps we should take a closer look at these measure formulae. Do they have a more general significance?
Categories of knowing represented by the measure formulae
What are these measure formulae, position and its derivatives, velocity and acceleration? Are they just the simple "physical quantities," as they are referred to in the textbooks?
Not so. Closer examination reveals fundamental qualitative differences between them. To understand this, consider how each of these measures is known. Position can only be observed visually or by less direct processes. Velocity is an intellectual abstraction: it cannot be known from direct experience. It must be computed. To know velocity, we must make two observations of position, determine their differences, and divide the time elapsed, thus obtaining a ratio. (Though velocity can be read from a speedometer, the only accurate speedometer, a chronometric tachometer, is itself a computer.) The velocity of the airplane even at six hundred miles an hour is something that one is completely unaware of. The earth is "hurtling" through space at eighteen miles per second, yet we have no feeling of it.
Acceleration, however, is felt. For example, when an elevator suddenly starts down, you feel it in the pit of your stomach; when the airplane comes in for a landing and the jets are reversed, you are thrown forward in your seat. Acceleration may also be computed, but it can be directly and physically experienced by the knower because the nervous system registers change, not a steady state.
The notion of velocity is so far removed from direct human experience that it was not until after Newton's discoveries that it became a formally recognized concept. And for all its acceptance by modern civilizations, velocity is nevertheless denied by many philosophers, because it is neither an "event" nor an "individual."*
*For an example of the confusion that exists over this question. see Smart. J. J. C.. Problems of Time and Space. New York: Macmillan. 1964.
We may deny the reality if we wish, although it would then be hard to know which of the formulae we might endow with reality. In any case, this misses the point. What is important is that:
1. Position, velocity, and acceleration are separate and different aspects of the total situation.
2. They are all necessary.
3. They are included in the scientific description.
4. And most important, they are different categories of knowing. Position is observed, velocity is computed, acceleration is felt. Control, the fourth category, is essentially indeterminate.
The scientific basis for the human faculties
The fundamental differences between the measure formulae, demonstrated by the different ways they are known, suggest that the origin of feeling, thought, and sensation may not be merely human, but may lie much deeper.
When we describe the human organism in this way, however, we are in double jeopardy. The behaviorist says: "You see, the human organism is merely a machine"; while the vitalist counters: "When you try to prove that man is merely a machine, you deny free will."
We would answer both points of view by referring to the fourth aspect, control. In a machine, this would include all the devices provided for its control: the accelerating, braking, and steering mechanisms. But all the mechanisms, no matter how elaborate, do not complete the control. Control must be initiated by an operator. And this absolutely essential element is indeterminate and unknowable to an observer.
Thus the complete account, far from denying free will, shows both the possibility of free will and the requirements for its effective operation. For if any of the three "mechanical" aspects does not function properly or is tampered with by an enemy agent or even a behaviorist, free will cannot manifest itself.
The learning cycle
The learning cycle further illustrates the cycle of action. An infant begins with a spontaneous act. He reaches out to grab something (1). Then he encounters a painful contact, perhaps a hot stove, and he reacts by withdrawing his hand (2). After the pain subsides, he takes stock, associates the stove with pain, observes the situation (3). Finally, he controls his action by avoiding hot stoves (4).
The four types of action in the learning cycle correspond to the four measure formulae:
Spontaneous act (impulse) = acceleration
Reaction (also spontaneous) = velocity (i.e., change)
Observation = position (the observable factor)
Control = control
The same diagram that we used to depict the cycle of action may be used to represent the learning cycle, but it is necessary to reverse the clockwise order and to start at the left:
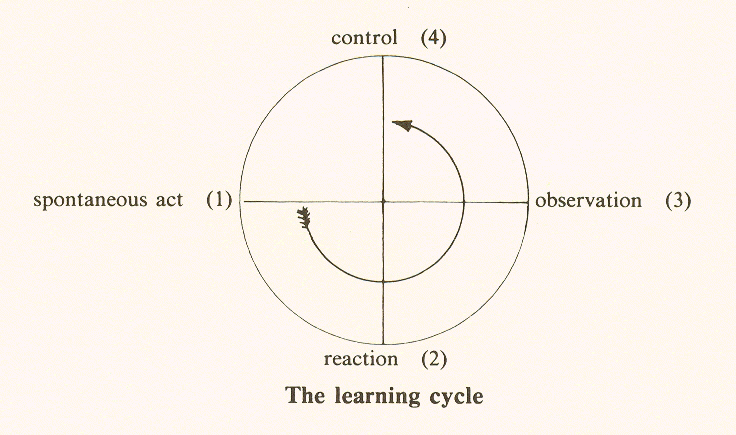
While it is satisfying that the same scheme serves to represent such dissimilar activities as an operator's controlling a machine and a child's learning about the world, the fact that the order must be reversed is important and will be discussed later. Another indication of incompleteness is that, so far, we have dealt only with actions, each of which is part of a larger cycle which begins with a stimulus and leads to a result. The behaviorists, in their dependence on the duality of stimulus and response (a form of action), fail to recognize the necessity of a third factor: when a dog's hunger is satisfied, it may no longer respond to the stimulus of food.
But when the stimulus causes wrong action and the result is not achieved, the learning cycle becomes necessary. Thus the learning cycle occurs only when there is an obstacle in the larger, threefold cycle.