
*
COMPARISON OF THREEFOLD AND FOURFOLD OPERATORS
An important property of the threefold operator is its nonfiniteness. This property comes about because non finiteness is simpler than finiteness.

We may think of the threefold as an endless line. Between any two points on this line, we can say which is before, but we cannot look at a piece of it without getting off the line.
Any cut-off line limiting the infinite extension A-B (in fact, any indication even of position on the line) requires another dimension crossing the line. This new dimension, plus the line itself, takes us into a different world, the two-dimensional space of measure and analysis (the fourfold).
The threefold is but one dimension, flowing perpetually in one direction like a point on a line, its past having one kind of existence, its future another, and the point itself a third.* This is experienced time, prior to clocks and measure. It is a reality which is always with us, yet perpetually eludes analytic description. Why, we might ask, does scientific description give it so little attention?** It is the old story: since it has no contrary, it cannot be isolated and subjected to analysis. Though we pour it from vessel to vessel, we never see it move.
*In view of the one-dimensionality of the threefold, it may seem odd that we found three dimensions necessary for its representation. This can be reconciled, however, by thinking of the line as curving through space in an arbitrary fashion. It remains a one-dimensional line, even though its domain has three dimensions. As we will show later, this line is a constraint in one dimension but is free in two, whereas the plane is a constraint of two dimensions but free in one.
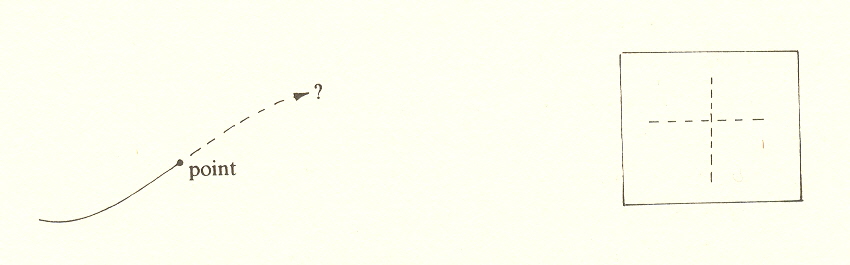
**As a matter of fact, science does recognize the asymmetry of time in the second law of thermodynamics, which states that entropy is positive (energy tends to become more evenly distributed). This is a sort of "black sheep" in the family of scientific law, both because it makes time asymmetric and because it cannot be deduced theoretically.
If we try to analyze what it is that the threefold describes, we are in a bind, for it is just that element of participation in life that analysis cannot, and does not even pretend to, cope with.
If the threefold describes the "active element," it does so only by pointing to it; it does not describe it in the way a map describes the relation of points on a surface. The description given by a map is not a substitute for the relationships of points described; it is that relationship. The relation of points on a map is less ambiguous than the relation of places in the landscape. On the other hand, the definition of love as "the attraction of one person for another" also describes a relation, but the definition is completely devoid of the content of actual love. In the case of the map, the lack of content is irrelevant.
The fourfold expresses the aspects of a situation. But the shift from one mode of being to another, from action to the result toward which the action is directed, is the realm of the threefold. What it describes or refers to is the interconnectedness of modes of being for which categories or names of any sort are only keys, and do not provide sufficient description.
This is why the Zen master, when asked the nature of the Buddha, strikes the student on the head with a stick. No words can convey participation or the realization to which participation can lead. The words, the analysis, are a screen through which action penetrates (see the second diagram below) bringing the action into a new state. The threefold "stands for" all this-not in the sense that it defines it, but in the sense that its intrinsic dynamic is of the same order, time-like rather than space-like.
Two models come to mind for illustration of the threefold:
This hourglass model has the merit of emphasizing the uniqueness of the present. But the plane of qualification penetrated by the line of motion is an equally valid representation, and has the merit of showing the independence of the time line from the two dimensions which describe the plane.
Example from psychology
The study of perception provides a good example of the distinction between the three- and fourfold. If I draw a diagram on a sheet of paper to show what a square is, what actually happens is a series of occurrences, point events in time. The square itself is a different kind of thing, and exists only after we have integrated a series of instances and fitted them into a meaningful pattern. The square has no real existence, any more than the Big Dipper has real existence. The eye does not see the square; rather it follows the line that describes it, as did the pen that drew it. Something other than the eye-call it the mind-integrates this motion, compares it with other known shapes, and decides it's a square.
Von Senden* collected reports on a number of persons who had been blind since birth and then received their sight by means of an operation. He found an inability to detect the difference between a circle and a triangle. Months of training were required before the difference could be recognized. This indicates that the image transmitted by the eye must be integrated, and that this process must be learned. We do not even need to say by what. We can define mind as "that which integrates sensation and form."
*Von Senden, M. Raum- und Gestaltauffassung bei operieten Blindgeborenen vor und nach der Operation. Leipzig: Barth, 1932.
Direct experience, the threefold, is prior to perception.
This supports Kant's description of time and space as a priori. However, there is no basis for assuming that it is time or space separately that is a priori,' it is rather the linear succession of events in time that is a priori, or, as I would prefer to say, accompanies experience. This may be called subjective time or it may be called pure time.* But when the eye follows the outline of a square, the experience is one of movement, of time and space undifferentiated. Even if the person feels the outline of a square or walks around one, the immediate experience is a series of events in subjective time. The only order he can draw upon (when he comes to integrate) is this sequential time ordering, which does not become measurable or "space-like" until the mind compares one experience with another.**
*Time as directly apprehended before measure or analysis.
**Such comparison requires that we look at two things simultaneously. The matrix of this simultaneous difference is space.
I prefer to call this time flow extension, meaning that it is the a priori basis for measure of either time or space. As an aid to abandoning the notion that time and space are independent realities (whereas, in fact, they are only separate concepts), recall that almost all primitive measures of distance are in terms of time. A place is so many days' journey, etc. One measure of distance that I particularly like is used by the Yakuts, who inhabit the tundras of northern Siberia. Their unit is "the distance a man can walk out and back while a pot is coming to a boil."
Constraint and freedom
There is another important distinction between the three- and fourfold which is implied by their one- and two-dimensional natures.
Suppose I say, "I'll meet you at 18th and Walnut." I have specified a place but not a time. Two dimensions are committed because "18th and Walnut" is a position on the earth's surface (latitude and longitude). Commitment in space imposes two degrees of constraint.
Only if I specify both time and place can our meeting occur in fact. Three degrees of constraint are necessary. Three dimensions must be committed, one in time and two in space.
In view of the three-dimensionality of space, one might suppose that it requires three dimensions to describe position. It can be shown that one of these three dimensions is unnecessary, but I will not take the time here for the proof.*
*To intercept an enemy missile, for example, we would use two dimensions to point the gun (a horizontal and a vertical angle). The third dimension in a radial direction combines distance with time of flight and doesn't need to be separated into time and space.
The notion of degrees of constraint may seem to be opposed to the more commonly used degrees of freedom. We say the two dimensions needed to describe form are constraints, while it is usual to think of the plane as having two degrees of freedom. Actually, there is no conflict here. The point is that the plane has two dimensions, which may be either free or constrained; when a position is specified, two degrees are constrained. Similarly, the line has one dimension which, when specified, imposes one degree of constraint.
The threefold and fourfold operators, then, may be thought of as using up or removing the freedom implicit in the three dimensions. The combination of three- and fourfold applies to the physical space-time world of objects and events. This is the world of determinism, subject to all the laws of classical physics.
We may diagram the situation thus:
Level Character Freedom
I Unity Three dimensions free
II Threefold One dimension committed, two free
III Fourfold Two dimensions committed, one free
IV Twelvefold Three dimensions committed, determinism
The threefold has one dimension committed (time). The fourfold has two dimensions committed (mental space). The twelvefold has three dimensions committed (actual space-time).
Order of the realms
Part of our quest has been to find an order. We found that the four aspects were equally important to a total situation and hence did not establish an order. We then took up the basic parameters of physics, M, L, and T, whose combination produced the measure formulae. Using these fundamental "simples" of physics to divide the whole in different ways provided the order we require. And the implications are plain.
Threefold precedes fourfold, and both precede their conjunction in the twelvefold realm of physical matter. Applied to the ontology of human existence, experience precedes mind, and both precede sense data.*
*This statement seems both to confirm and deny Hume, who said that sense experience preceded mind. Our position is that experience is essentially internal and a priori, i.e., pleasure and pain are induced, not produced by external events. And it is only after mind has constructed itself (by integrating experience, i.e., association of pain or pleasure with specific objects) that sensation, in the sense of information from the outer world, becomes possible.
Summary
To clarify the distinction between the threefold and fourfold operators, as applied to ontology, I have listed them in a comparison chart:*
Threefold (experience, feeling) Fourfold (concepts, intellect)
Indefinite, infinite Finite
One dimension committed, Two dimensions committed,
two dimensions free one dimension free
Asymmetrical Symmetrical
Irreversible Reversible
Exists in time (sequence) Exists in space (simultaneous)
Ordering can be taken only Ordering possible in any
one way direction
The matrix of experience The matrix of mind
Supplies substance,* Supplies measure, form,
motion, and value and concept
Requires three dimensions Requires only two dimensions
for full representation for full representation
*Substance will be described in Chapter VIII.
We may sum this up by saying "Time supplies content - space supplies measure." The magnitude of space depends ultimately on time to traverse it. The measurement of time depends on treating it like space.
A philosophical overview
Despite glimpses we may have had of its applicability or use, the device we have been constructing still seems rather aloof, incomprehensible, extraneous, remote from the predicament of men, whose experiences bear little resemblance to geometrical exercises. What use can there be in these abstract angles, these imaginary sections of the real that turn what is vivid and alive into something like a Renaissance drawing of figures and buildings in perspective, subservient to mere geometry?
One reads in science fiction of a visitor from outer space landing on this planet and constructing mysterious machines with rays of light, or, in old tales, of magicians drawing magic circles, waving wands, or conjuring Beelzebub with figures drawn in sand.
Why is it that virtually all of the highly developed cultures of the world have used as their symbol some geometric construction - be it the mandala of ancient Hinduism or the interlacing triangles of the Star of David?
Somewhere within us there is an instinct for this abstract world - a world that is in some sense outside life, yet upon which all life pivots; that supports it like the pins of a great steel door to a bank vault, so that if one but had the key, all would be open to him. This abstract world is at the core of our existence.
So let us have patience with the super-mathematician in us, so remote, so aloof, whom no noise or bluster can awaken, but who, when as Eddington says, "we announce we have found a group . . . of operations . . . some of which are square roots of minus one. . . ,"* begins to sit up and take notice.
*Eddington, Arthur S. New Pathways in Science. New York: Macmillan, 1935.
How may we show that there is any essential authority in the super- mathematician? Since our thinking has been based upon the meaning of the right angle, I might try to answer this question by citing an observation which struck me when I looked up the word "right" in the dictionary. The first two definitions of "right" are: (1) straight, not crooked; (2) upright, erect from a base. . . perpendicular.
What struck me about these definitions is the confusion between the moral sense of the word and the geometric sense. In fact, "straight, not crooked" could apply equally well to a line on a paper and a person's moral character. I take this confusion as a manifestation of a similarity in meaning which lies deeper than the word itself. This can be seen in the word "upright," which has connotations that are not exclusively geometrical. (Up and down are, from the point of view of geometry, relative.) In order to stand up, man has to exercise a continual counterpoise of muscles. His judgment is necessary to determine deviation from a vertical position, and he must exercise this counterpoise in order to remain "upright."
So then we can at least accept that the uniqueness of the right angle, in creating a dimension that is independent of an activity under consideration, provides the measure, the mean, and we can now say (in the light of four-ness) the meaning of the activity.
Our geometry of meaning may therefore be described as "a description of the right angle - its scope, application and significance."